The DNI number is used to uniquely identify us and is chosen in order from the set of numbers randomly provided by the General Directorate of Police for each police station. However, the letter is determined, from the assigned number, according to a mathematical algorithm. This detects potential errors and forgeries.
This algorithm is based on something called modular or clock arithmetic, which is used to describe cyclical processes, such as the passage of time by hours of the day, days, or months. After twelve o’clock, one o’clock again, after the last day of the month, the first day again, and at the end of December begins January. In this arithmetic process we calculate in a cyclical way, that is, when we reach a certain number – which we call the unit – we start again.
We can imagine it as a clock whose clocks are consecutive integers, which we pass through periodically. Of course, these hours do not have to contain 12 hours, but we can create them with any integer. In addition, they have another peculiarity: we start counting from zero, so an hour, for example, eight hours, has numbers from zero to seven.
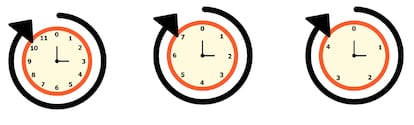
Standard arithmetic was first systematically studied by Carl Friedrich Gauss in his famous book Computational discoveries From 1801. Gauss defined congruence as follows: two integers a and b are congruent to another number n if the remainder of division (without decimals) a and b by n is the same. This is equivalent to b – a multiple of n. For example, 6 and 18 are congruent modes of 12. That is, when dividing 6 by 12, we get 0 as the quotient and 6 as the remainder, on the other hand, when dividing 18 by 12, we are left with a quotient of 1 and also a remainder of 6. In o’clock, that means 18 is 6.

As in our usual numbering, in modular arithmetic we can also operate: If we have two pairs of numbers that are congruent noThis will be their sums. The same applies to subtraction and multiplication.
For DNI, modulo match 23 is used. The procedure consists in calculating the remainder of dividing the DNI number by 23. Based on this remainder, a letter is assigned according to the table shown in the image below.

Thus, if we make a small mistake when entering our ID card, the new number will not correspond to the entered character and a warning will appear on any computer. But why are only 23 letters used and not the entire alphabet? The letters O and I are ignored because of their great similarity to 0 and 1. On the other hand, the letters Ñ may cause problems abroad. If we consider the remaining 24 characters, the process will not be reliable enough. This is due to the large number of divisors that the number 24 has.
In particular, if we change a number, we can get two numbers that have the same character assigned to them. Suppose we change a number in the first five by adding or subtracting 3, for example, if we write 27526803 instead of 27523803. By making this change, the difference from the original number is 3 followed by at least three zeros (for example, in our case, 3000), which is always a multiple of 24. Therefore, both numbers are identical to the scale of 24 and correspond to the same letter.
However, given unit 23, which is a prime number, this kind of error cannot occur. By changing one digit, the difference between the two numbers is the ones followed by the zeros, which will never be a multiple of 23. So any letter, the U, is omitted, leaving us with 23 and a more reliable system.
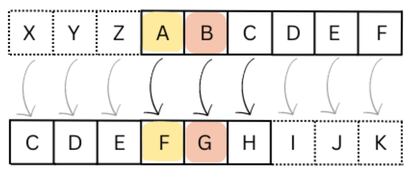
The DNI is not the only control number that is calculated by matching: also the IBAN for bank accounts. Moreover, this account is of great importance in cryptography. Without going any further, the classic Caesar cipher, which consists of moving the alphabet a fixed number of positions, is a straightforward application of matching. For example, in Caesar 5, each letter is changed to the letter found five later, that is, A is changed to F, B to G, and so on. We are working in scale 27, so the last letters of the alphabet will be changed to the first. For example, “match” can be written as “Htrlwzjrhnfx”. Other, more modern and secure methods, such as RSA, also based on congruence. This uses more complex properties of modular arithmetic, such as the presence and properties of inverse elements.
Alba Garcia Ruiz And Javier Penafiel Predoctoral researchers at the Institute of Mathematical Sciences
Coffee and theories is a section dedicated to mathematics and the environment in which it was created, coordinated by the Institute of Mathematical Sciences (ICMAT), in which researchers and members of the center describe the latest developments in this discipline, share points of convergence between mathematics and other social and cultural expressions and remember those who marked their development and knew how to turn coffee into theories . The name evokes Hungarian mathematician Alfred Rennie’s definition: “A mathematician is a machine that turns coffee into theorems.”
Edition and format: Agata A. Timón G Longoria (ICMAT).
You can follow Theme in FacebookAnd Twitter And instagramor register here to receive Weekly newsletter.

“Beeraholic. Friend of animals everywhere. Evil web scholar. Zombie maven.”
